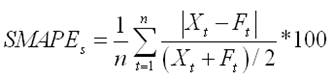|
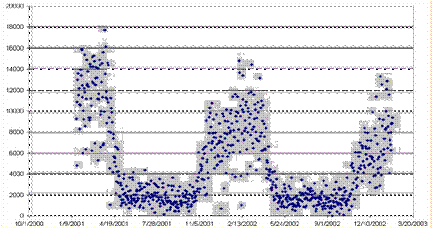
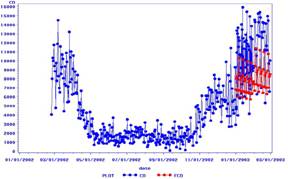
NN5 Motivation This competition is an extension of the earlier NN3 forecasting competition for neural networks and methods of computational intelligence, funded as the 2005/2006 SAS & International Institute of Forecasters research grant for "Automatic Modelling and Forecasting with Neural Networks – A forecasting competition evaluation" to support research on principles of forecasting. The competition has been extended towards datasets with different time series frequency using a constant competition design. 1. NN5 Description of the problem addressed We seek to evaluate the accuracy of computational intelligence (CI) methods in time series forecasting on a set of 11 and 111 daily empirical time series of cash-machine withdrawals at different locations in the UK, such as the one displayed in fig.1. Fig.1. Example time series of cash withdrawals at an ATM The data represents cash money withdrawals taken at various automatic teller machines (ATMs, or cash machine) in England. Cash machines operate as miniature “retail outlets” with regional specifics driving the demand for cash in competition to other ATMs in the vicinity. Cash demand needs to be forecasted accurately similar to other products in vending machines, as an inventory of cash money needs to be ordered and replenished for a set period of time beforehand. If the forecasts are flawed, they induce costs: is the forecast too high unused money is stored in the ATM incurring costs to the institution; if the ATM runs out of cash, profit is lost and customers are dissatisfied. The data will reflect a number of time series patterns of multiple overlying seasonality, local trends and structural breaks that are driven by unobserved causal forces driven by the underlying yearly calendar, such as reoccurring holiday periods (e.g. an ATM in a holiday resort will exhibit a yearly seasonality, one located in a conference center one related to events of difference size), bank holidays with different lead and lag effects (e.g. Labour Day, Easter, Christmas), or special events of different length and magnitude of impact. These may impact the time series with varying lead and lag effects and may require identifying obsolete data to prevent producing biased forecasts. In addition, the data can contain one-time outliers, outlier patches, missing values and structural breaks such as level shifts, changing seasonality or local time trends overlying the data structure containing the causal patterns (e.g. a new mall opens across the street from an ATM machine, and all historical data becomes obsolete). This will require a simultaneous identification and estimation during the modeling and training of the forecasting method. Moreover, the cash demand of each ATM may be driven in part by its physical location (mall, hotel, conference centre etc.), requiring an individual modeling approach for each time series. The task is in predictive modeling for regression using time series data. A training set of time ordered observations y1, y2, …, yt of the target variable y representing cash demand at a specific ATM is provided (see e.g. fig. 2.a). The objective of the competition is to predict the next unknown realizations yt+1, yt+2, …, yt+h of the target variable y for h time periods t (t=1,…,h) into the future (fig. 2.b).
Fig.2. ATM Training data (a.) and predictions from one time origin (b.) The task can only be achieved if the (singular or time reoccurring) external forces driving the data generating process are identified from the data itself, modeled and extrapolated for unseen data into the future. From the structure of the included variables an explanation on the forces may be derived, but the objective here is predictive accuracy, not explanatory power nor interpretability. 2. General Motivation, scientific merit, and expected impact on computational intelligence The past 20 years of research have led to more than 4000 publications on Computational Intelligence (CI) for time series forecasting, with an emphasis on artificial Neural Networks (NN) across various disciplines (Crone and Graffeille, 2004). A myriad of optimistic publications has indicated superior performance of NN on single time series (Adya and Collopy, 1998, Zhang et al., 1998) or small subsets (Hill et al., 1996). In contrast, their performance on forecasting a representative and homogeneous sample of time series data in objective competitions with state-of-statistical the-art benchmarks fell far shot of the presumed potential. The results of the large scale M3 competition using 3003 time series (Makridakis and Hibon 2000) have indicated the poor performance of NN for forecasting a large number of yearly, quarterly and monthly empirical time series multiple steps into the future. Following an initial interest by various NN research groups (Hibon, 2005), only (Balkin and Ord, 2000) successfully submitted NN results to the competition, outperforming only few of the more than twenty statistical and econometric competitor approaches. Recently, the NN3 competition (Crone, 2007; www.neural-forecasting-competition.com) revisited two subsets of 111 and 11 monthly time series used in the M3 competition to evaluate progress in modelling of NN and CI methods. The results indicate a substantial advancement and increase in performance from various CI methods, in particular though various forms of feedforward and recurrent NN ensembles. However, constant advances in econometric and statistical expert systems in other disciplines have led to benchmarks which proved hard to beat: only one contestant using recurrent NN outperformed the statistical expert software systems benchmarks, and only few contestants showed comparative performance. Although CI may show further promise if different approaches can be combined, on a level playing field of univariate time series forecasting statistics still outperforms CI. As a consequence, CI methods have not yet been established as a valid and reliable forecasting method in time series forecasting and are recently omitted in scientific and corporate applications. For example, Carreker, now part of CheckFree, has changed its forecasting platforms for cash money demand at ATMs from neural networks to SAS, then from SAS to Autobox, increasing forecasting accuracy and robustness in predicting cash demand at ATMs by 10%-500%. The main driver was the need to adapt to exogenous drivers: one time or reoccurring causal forces impacting the demand of cash money at ATMs. However, recent publications document competitive performance of NN on a larger number of time series (Liao and Fildes, 2005, Zhang and Qi, 2005, Crone, 2005), indicating the use of increased computational power to automate NN forecasting on a scale suitable for automatic forecasting. The majority of research in corporate forecasting using CI and statistical methods has focussed on single time series and low frequency data of a monthly level, trying to remedy the superiority of statistics on the monthly benchmarks. In contrast, CI has shown competitive performance in multivariate modelling using explanatory variables of high frequency data, e.g. 4 of the time series in the Santa Fe competition (Weigend, 1994), the EUNITE competition on electricity load forecasting (Suykens and Vandewalle, 1998), the ANNEXG competition on river flood forecasting (Dawson, 2001 and 2006) or the WCCI’06 Predictive Uncertainty competition (Gawley, 2006). However, most of the competitions were restricted to an evaluation on a single time series, ignoring evidence within the forecasting field on how to increase validity and reliability in evaluating forecasting methods (Fildes et al., 1998). In contrast, no competition in the forecasting and econometrics domain has evaluated multivariate, causal time series. As CI seems to perform better for time series with higher frequency, such as hourly, daily or weekly data, much of the effort of proving CI’s worth in experimental designs and competitions appears misdirected. This provides a research gap to objectively evaluate the performance of CI-methods on high frequency data outside the established domain of electricity load forecasting in a representative competition. In addition, despite research by Remus and O'Connor (2001) little knowledge is disseminated on sound “principles” to assure valid and reliable modelling of NN for causal forecasting of high frequency data with the ever increasing number of NN and (hybrid) CI paradigms, architectures and extensions to existing models. Different research groups and application domains favour certain modelling paradigms, preferring specific data pre-processing techniques (differencing, deseasonalising, outlier correction or not), data sampling, model meta-parameters, rules to determine these parameters, training algorithms etc. However, the motivation for these decisions – derived from objective modelling recommendations, internal best practices or a subjective, heuristic and iterative modelling process - is rarely documented in publications. In addition, original research often focuses on the publication of (marginal) improvements to existing methods, instead of the comparison and consolidation of accepted heuristic methodologies. Therefore we seek to encourage the dissemination of implicit knowledge through demonstrations of current “best practices” methodology on a representative set of time series. Consequently, we propose a forecasting competition evaluating a set of consistent CI methodologies across a representative set of time series. We seek to propose two essential research questions, which may be resolved through inviting current experts in the CI academic community to participate in a causal forecasting competition:
Our previous competitions have attracted between 10 and 60 participants, with the 2007 NN3 competition attracting the largest competition participation in time series forecasting to date. Time series forecasting attracts a smaller audience then classification even including the statistical & econometrical field. These have raised the visibility and success of CI methods beyond the IEEE and CI domain, attracting researchers from various domains, and attracting large numbers of students and beginning researchers. Furthermore, this competition may serve as a test-bed for future competitions using an enhanced setup drawing upon experiences made during this competition, using a larger set of similar empirical data plus possible synthetic data in collaboration with interested parties and the IEEE CIS and the IEEE CIS DMTC, or as part of a larger “grand challenge”. This should include a repeated set of competitions on small but homogeneous datasets to derive a ‘ranking’ of participating teams over the course of time to ensure higher validity and reliability of the results. 3. Experimental setup and/or data description Cash money demand represents a non-stationary, heteroscedastic process. The time series features, regular trend-seasonal and irregular structural components of the data as well as causal forces impacting on the data generating process were already indicated in section 1. The data will consist of a data set of 11 and 111 empirical time series of 2 years of daily data, provided by an unknown source. The data has not been used in previous competitions to prevent overfitting to the domain or dataset. All data is linearly scaled to ensure anonymity of the time series. The competition design and dataset adhere to previously identified requirements from major forecasting competitions in the statistics and econometrics domain (Fildes et al., 1998; Makridakis and Hibon, 2000) as well as set out through the International Journal of Forecasting and build upon experience from the preceding NN3-competition in the CI-domain in order to derive valid and reliable competition results:
4. Evaluation procedures and established baselines The evaluation of the competition will be conducted ex-post on the test set using a set of representative and unbiased forecasting error metrics in comparison to various benchmarks:
We assume no particular decision problem of the underlying forecasting competition and hence assume symmetric cost of errors. To account for a different number of observations in the individual data sub-samples of training and test set, and the different scale between individual series we propose to use a mean percentage error metric, which is also established best-practice in industry and in previous competitions. All submissions will be evaluated using the mean Symmteric Mean Absolute Percent Error (SMAPE) across all time series. The SMAPE calculates the absolute error in percent between the actuals X and the forecast F across all observations t of the test set of size n for each time series s:
The SMAPE of each series will then be averaged over all time series in the dataset for a mean SMAPE. To determine a winner, all submissions will be ranked by mean SMAPE across all series. However, biases may be introduced in selecting a “best” method based upon a single metric, particularly in the lack of a true objective or loss function. Therefore, while our primary means of ranking forecasting approaches is mean SMAPE, alternative metrics will be used so as to guarantee the integrity of the presented results. For reporting purposes all submitted forecasts will also be evaluated on a number of additional statistical error measures to analyze sensitivity to the metrics itself, including:
The competition is open to all methods from CI. The objective requires a single methodology, which is implemented across all time series. This does not require a single configuration, i.e. one NN with a pre-specified input-, hidden and output-node structure, but a process in which to run tests and determine a best setup for each time series. On the same data sample, the process should always lead to selecting the same final model structure as a rigorous process. The methods include, but are not limited to:
These will be evaluated against established statistical forecasting methods and benchmark expert system software packages:
Statistical benchmarks will be calculated using the software ForecastPro, one of the leading expert system software packages for automatic forecasting (by Eric Stellwagen, CEO of Business Forecasting Systems) and Autobox (by David Reily, CEO of Automatic Forecasting Systems). Selected References
|
|